椭球面上的测量计算
1.地球椭球的基本参数与关系
1.1基本参数
长半轴 a
短半轴 b
扁率 $α=\frac{a-b}{a}$
第一偏心率 e=\(\frac{\sqrt{a^2-b^2}}{a} \)
第一偏心率 e’=\(\frac{\sqrt{a^2-b^2}}{b} \)
为了简化书写,我们还引入一下符号:
\(c = \frac{a^2}{b} \), \(t = tanB \), \(η = e’^2cos^2B \)
此外,还有两个常用的辅助函数:
$W = \sqrt{1 - e^2sin^2B}$
$V = \sqrt{1+e’^2cos^2B}$
1.2相互关系
略。。。。
2.1常用坐标系
大地坐标系
用(L,B,H)表示。
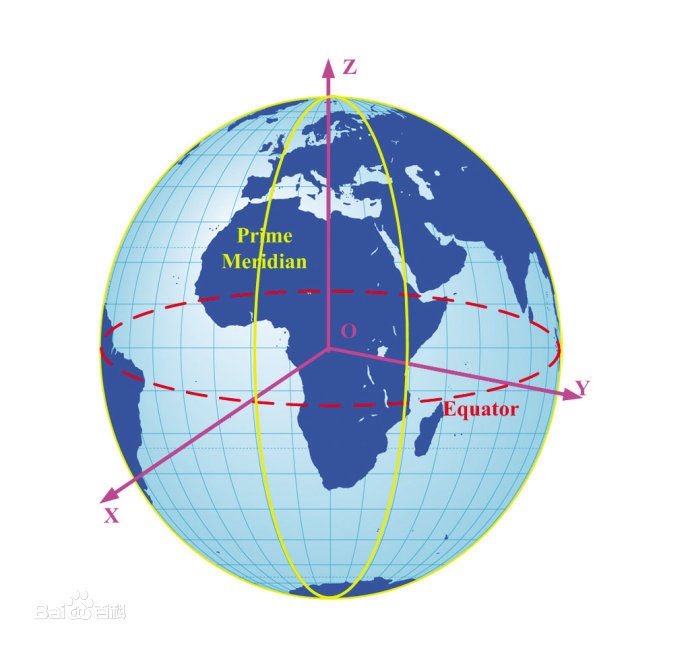
空间直角坐标系
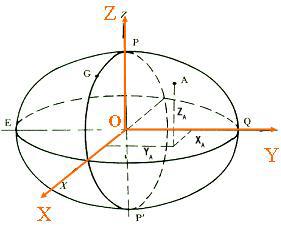
子午面直角坐标系
用(L,X,Y)表示。
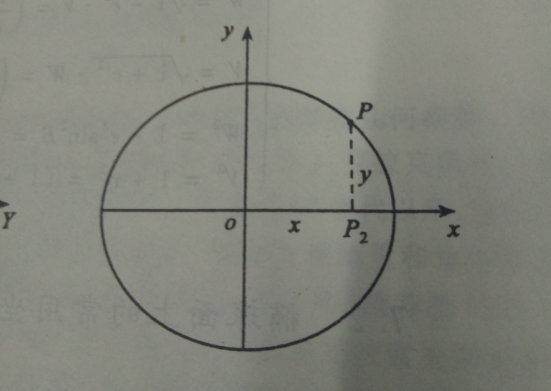
地心维度坐标系
用(L,φ,ρ)表示。
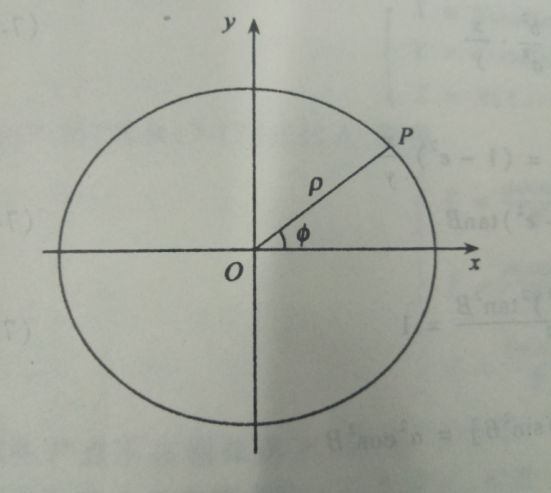
大地极坐标系
用(S,A)表示。S为大底线长度,A为大地方位角。
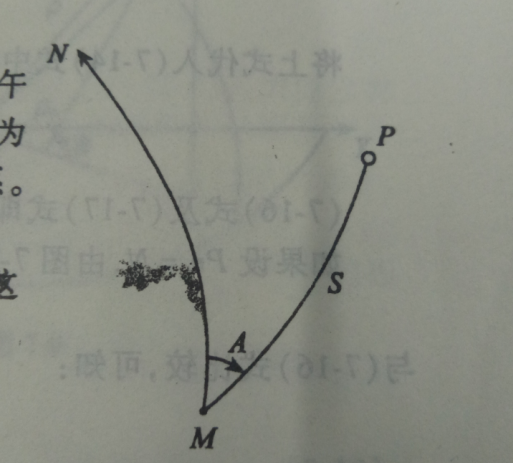
2.2坐标系关系
见书P5。
子午面直角坐标系与大地坐标系 –>空间直角坐标系与子午面直角坐标系 –>空间直角坐标系与大地坐标系
子午面直角坐标系与大地坐标系:
$x = \frac{acosB}{\sqrt{1-e^2sin^2B}} = \frac{acosB}{W}$
$y = \frac{bsinB}{V}$
$x = NcosB$ (N为Pn,书上P5。)
$y = N(1-e^2)$
空间直角坐标系与子午面直角坐标系:
$X = xcosL$
$Y = xsinL$
$Z = y$
空间直角坐标系与大地坐标系:
$X = NcosBcosL$
$Y = NcosBsinL$
$Z = N(1-e^2)sinB$
$X = \frac{acosB}{W}cosL$
$Y = \frac{acosB}{W}sinL$
$Z = \frac{bsinB}{V})$
有大地高H时:
$X = (N+H)cosBcosL$
$Y = (N+H)cosBsinL$
$Z = (N(1-e^2)+H)sinB$
问题:外法线矢量单位怎么得来的?
3.椭球面上的几种曲率半径
3.1子午圈曲率半径
$M = \frac{a(1-e^2)}{W^3} , M = \frac{c}{V^3} , M = \frac{N}{V^2}$
3.2卯酋圈曲率半径
$Pn = N = \frac{a}{W} = \frac{r}{cosB}$
3.3主曲率半径的计算
$M = \frac{a(1-e^2)}{W^3} = a(1-e^2)(1-e^2sin^2B)^\frac{-3}{2}$
$N = \frac{a}{W} = a(1-e^2sin^2B)^\frac{-1}{2}$
将这两个式子级数展开、、、
牛顿二项式定理:
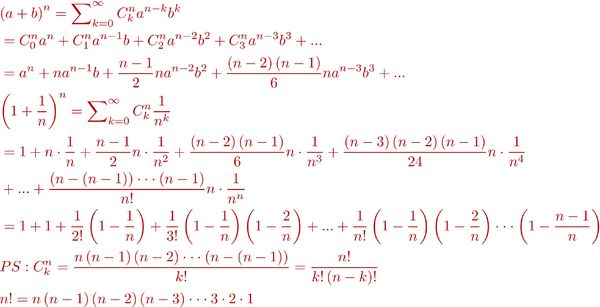
问题:怎么展开的?
3.4任意法截弧的曲率半径
尤拉公式 $\frac{1}{R_A}= \frac{cos^2A}{M}+\frac{sin^2A}{N}$
改写 RA $= \frac{MN}{Ncos^2A+Msin^2A}$
由$\frac{N}{M} = V^2 = 1+ η^2$
得 RA $= \frac{N}{1+η^2cos^2A} = \frac{N}{1+e’^2cos^2Bcos^2A}$
3.5平均曲率半径
$R = \frac{N}{V} = \frac{c}{V^2} = \sqrt{MN}$
3.6M,N,R的关系
$N>R>M$
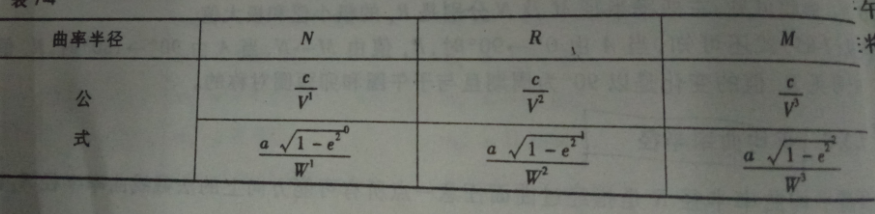
4.椭球面上的弧长计算
4.1子午线的弧长计算
$X = \int^B_0MdB$
$X = a_0B - \frac{a_2}{2}sin2B+ \frac{a_4}{4}sin4B- \frac{a_6}{6}sin6B+ \frac{a_8}{8}sin8B$
$a_0…a_8$的值见书P17。
问题:公式的推导过程?
4.2由子午线求大地纬度
4.3平行圈弧长计算
$r = x = NcosB = \frac{acosB}{\sqrt{1-e^2sin^2B}}$
$S = rl = NcosBl’’ = b_1l’’$ ($l’’ = L_1-L_2$,$b_1=\frac{NcosB}{ρ’’}$可以以B为引数从《高斯投影坐标计算表》中查取。)
问题:平行圈弧长纵向变化?
4.4子午线弧长和平行圈弧长变化比较
略
4.5椭球面梯形图幅面积计算
问题:未看?
5.大地线
5.1相对法截线
法截线:法截面与曲面交汇形成的曲线。
通常情况下,正反法截线是不重合的。因此在椭球面上A,B,C三个点测得的角度不能构成闭合三角形。
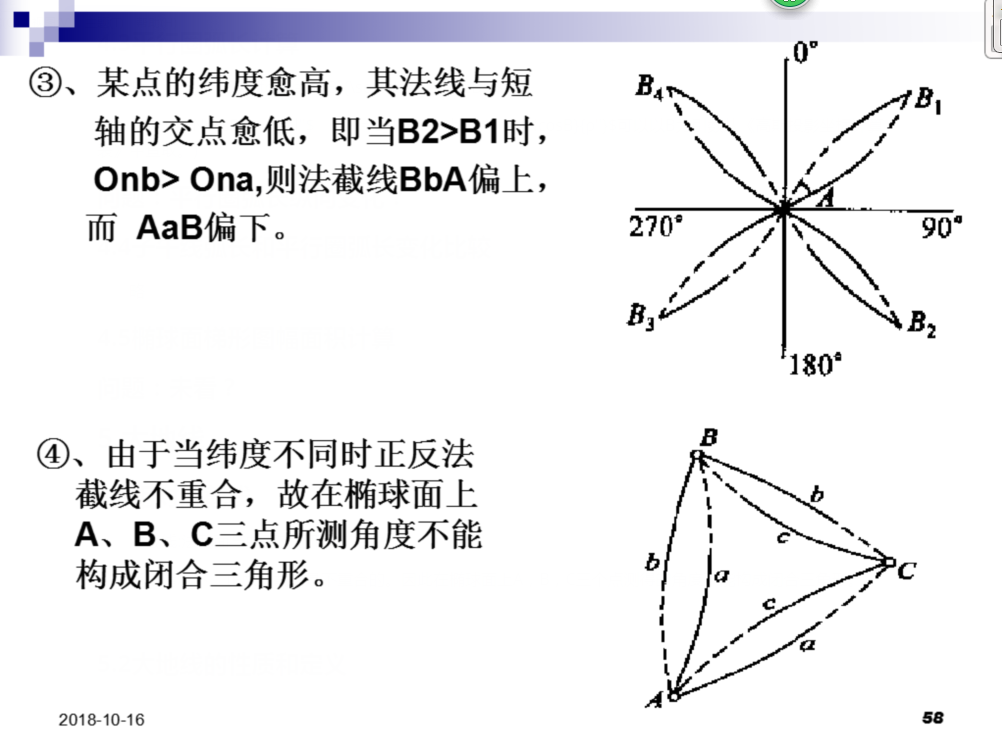
5.2大地线的性质和定义

问题:曲线的夹角怎么算?
5.3大地线微分方程和克莱劳方程
大地线微分方程:
$\frac{dB}{dS} = \frac{cosA}{M}$
$\frac{dL}{dS} = \frac{sinA}{NcosB}$
$\frac{dA}{dS} = \frac{sinAtanB}{N}$
克莱劳方程:
$r·sinA = C$ C为大地线常数。
6.将地面观测值归算至椭球面
6.1将地面观测的水平方向归算至椭球面
三差改正:
$δ_u” = - (ξ”sinA_m - η”cosA_m)cotZ_1$
$δ_u” = - (ξ”sinA_m - η”cosA_m)tanα_1$

- 标高差改正$δ_h$
