椭球面元素归算至高斯平面

1.地图学投影变换基本概念

1.1投影变换的意义和方程

$x = F_1(L,B)$

$y = F_2(L,B)$

1.2地图投影的变形

• 长度比

$m = \lim_{P_1P_2\rightarrow0} \frac{P_1’P_2’}{P_1P_2}$

结论：一点的长度比，不仅随点的位置，而且随线段方向而变化。

• 主方向和变形椭圆

$ m = r $(r为变形椭圆半径，即O’P’)

• 投影变形

变形的基本特征

1. 长度变形

   $m = r = \sqrt{a^2cos^2α+b^2sin^2α}$ α为方位角。

   长度变形：$ v = m-1$

2. 方向变形

   投影后方位角减去原来的方位角的差值称为方向变形。

   计算方向变形公式：$sin(α-α’) = \frac{a-b}{a+b}sin(α+α’)$

   最大方向变形公式：$tanα_0 = \pm\sqrt{\frac{a}{b}},tanα’_0 = \pm\sqrt{\frac{b}{a}}$

3. 角度变形

   计算变形公式：$△u = u’-u = 2(α_1-α’_1)$

   最大角度变形：$△u = 2ω =2arcsin\frac{a-b}{a+b}$

4. 面积变形

   投影面积比：$P = \frac{πab}{π}= ab$

   面积变形：$P-1$

1.3地图投影分类

• 按性质分类
  1. 等角投影
  2. 等积投影
  3. 任意投影
• 按投影形状分类
  1. 方位投影
  2. 圆锥投影
  3. 圆柱投影

2.高斯投影概述

2.1控制测量对地图投影的要求

• 采用等角投
• 限制在不大的范围内，从而控制变形并能用简单的公式计算其改正数。
• 将大的区域按一定规律分成若干个小区域。每个带单独投影，并组成本身的直角坐标系，然后再将这些简单的数学方法链接在一起，从而组成统一的系统。

2.2高斯投影基本概念

高斯投影

2.3椭球面三角系化算到高斯平面

略

3.正形投影的一般条件

柯西黎曼条件：

$\frac{\partial x}{\partial q} = \frac{\partial y}{\partial l}$

$\frac{\partial x}{\partial l} = -\frac{\partial y}{\partial q}$

---

$\frac{\partial x}{\partial B} = \frac{M\partial y}{NcosB\partial L}$

$\frac{\partial y}{\partial B} = -\frac{M\partial x}{NcosB\partial L}$

4.高斯投影坐标正反算公式

4.1正算

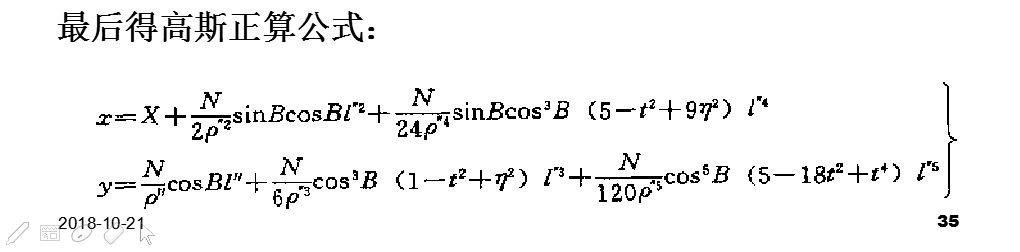
4.2反算

4.3几何解释

---

• ← Previous Post
• Next Post →