条件平差与间接平差

平差基础

必要观测数，用t表示，为独立量。一个几何模型独立量最多为t个。n为观测值个数，r为多余观测数，r=n-t。r又称为“自由度”。
除t个独立量以外，每增加一个量就产生一个函数关系式，被称为条件方程。一个几何模型如果有r个多余观测量，就产生r个条件方程。
仅用观测值组成条件，就会产生闭合差。如：$L_1+L_2+L_3-180=W\ne0$(三角形内角和)W即为闭合差。测量平差的主要目的就是消除闭合差。
$\tilde{L}$真值，$\hat{L}$平差值。
观测量是一个随机变量，描述随机变量的精度指标是方差（中误差），描述两个随机变量之间的相关性质是协方差。

条件平差

概念：以条件方程为函数模型的平差方法，称为条件平差方法。

步骤：

根据平差问题列出条件方程式，条件方程式个数等于多余观测数r。
根据条件式的系数，闭合差及观测值的协因数阵组成法方程式，法方程个数等于多余观测数r。
解算法方程，求出系数K值。
将K代入改正数方程式，求出V值，并求出平差值$\hat{L}=L+V$。
为了检测平差计算正确性，用平差值$\hat{L}$重新列出平差值条件方程式验算。

例题分析：例5-1 （P82）

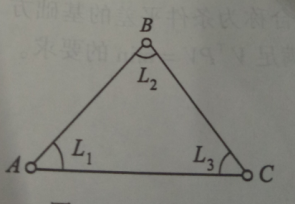
由题目可以列出一个条件方程：

$\hat{L_1}+\hat{L_2}+\hat{L_3}-180°=0$

将$\hat{L_i}=L_i+vi$代入上式得：

$v1+v2+v3+9=0$

总结：条件平差就是列出条件方程后，写为改正数加闭合差的形式（$AV+W=0$）,法方程为：$AP^{1}A^TK+W=0$。求出矩阵K。然后根据$V=P^{-1}A^TK=QA^TK$求出V（改正数）。平差值$\hat{L}=L+V$

间接平差

概念：选择几何模型中t个独立量为平差参数，将每个观测量表达成所选参数的函数，列出n个这种函数关系式，称为观测方程，以此为平差的函数模型称为间接平差法，又称为参数平差。

步骤：

根据平差问题，选择t个独立量做参数。
将每一个观测量的平差值分别表达成所选参数的函数，若函数非线性要先线性化，列出误差方程。
由误差方程系数B和自由项l组成法方程，法方程个数等于参数个数。
解算法方程，求出$\hat{x}$，计算参数的平差值$\hat{X}=X^o+\hat{x}$。
由误差方程计算V，求出观测平差值$\hat{L}=L+V$。

例题分析：例7-1（P114）

由题目知t=3，设BCD高程（平差值）分别为X1，X2，X3。写出5个平差方程:
l1 + v1 = X1 - HA
…
l5 + v5 = X3 - HA

由上式得误差方程:
v1 = X1 - (HA+L1)
…
v5 = X3 - (HA+L5)

BCD三点近似值可以表示为：

$X_1^0 = HA +l1$

$X_2^0 = HA +l3$

$X_3^0 = HA +l5$

所以：

$X1 = X_1^0+x_1=x_1+HA +l1$

$X2 = X_2^0+x_1=x_2+HA +l3$

$X3 = X_3^0+x_3=x_1+HA +l5$

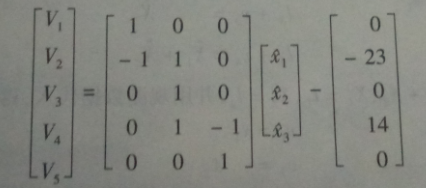
带入误差方程得：

v1 = $x_1$ + 0
…
v5 = $x_3$ + 0

改写为矩阵：

按10km为单位权，即：$P_i=\frac{C}{S_i}=\frac{10}{S_i}$

写出权阵：
$$
P = \left[
\begin{matrix}
2.9 & 0 & 0 & 0 & 0\
0 & 3.7 & 0 & 0 & 0\
7 & 0 & 2.5 & 0 & 0\
7 & 0 & 0 & 3.3 & 0\
7 & 0 & 0 & 0 & 4.0\
\end{matrix} \right]\tag{2}
$$

条件平差与间接平差